Кубическое уравнение. Решение кубических уравнений онлайн. Кубическое уравнение, алгебраическое уравнение третьей степени. Общий вид кубического уравнения: ax3 + bx2+ cx + d = 0, где а ≠ 0. Заменяя в этом уравнении х новым неизвестным у, связанным с х равенством х = у - b / 3a, кубическое уравнение можно привести к более простому (каноническому) виду: y3 + py + q = 0, где p = -b2 / 3a2 + c / a, q = 2b / 27a3- bc / 3a2 + d / a, решение же этого уравнения можно получить с помощью формулы Кардано:
Если коэффициенты кубического уравнения — действительные числа, то вопрос о характере его корней зависит от знака выражения q2 / 4 + p3 / 27, стоящего под квадратным корнем в формуле Кардано. Если q2 / 4 + p3 / 27>0, то кубическое уравнение имеет три различных корня: один из них действительный, два других — сопряжённые комплексные; если q2 / 4 + p3 / 27 =0, то все три корня действительны, два из них равны; если q2 / 4 + p3 / 27 <0, то все три корня действительны и различны. Выражение q2 / 4 + p3 / 27 только постоянным множителем отличается от дискриминанта кубического уравнения. D = - 4p3-27q2.
2008 - 2018. © My Planet - интересный сайт для всей семьи.
|




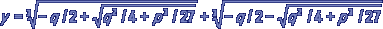 .
.